本文為機器學習模型建構的入門教學,將介紹如何運用線性迴歸模型預測特定區域的房屋售價。我們將從資料處理、模型設計、訓練到評估,逐步建構一個簡單線性迴歸模型(Simple Linear Regression Model),讓讀者能根據房屋特定的特徵預估其售價。透過本教學,你可以掌握建構此類模型所需的關鍵知識,包括特徵擷取、模型選擇、超參數設定、訓練模型的演算法,以及評估模型的方法。本主題將分為兩篇文章:上半部將探討資料處理與模型設計,下半部則著重於模型訓練與評估。
問題定義
模型的目標是預估特定區域房屋的售價。這有助於潛在買家、賣家或房地產經紀人對房屋價值有更客觀的判斷,從而做出更明智的決策。我們預測的目標變數(房屋售價)是一個連續的數值,因此這是一個典型的迴歸問題。
為了幫助初學者去理解機器學習模型的建構流程,本範例將採用最簡單的「簡單線性迴歸模型」來預測房屋售價。簡單線性迴歸的「簡單」指的是僅考慮單一資料屬性(變數)進行預測;而「線性」則表示在座標平面上,該特定變數與房價之呈現直線關係。
房屋銷售資料處理
本專案所使用的資料集,取自 Kaggle 平台,包含美國華盛頓州國王郡在 2014 年 5 月至 2015 年 5 月期間的房屋交易資料。在模型建構的資料處理階段,我們將依序執行以下關鍵步驟:
- 探索性資料分析(Exploratory Data Analysis,EDA)
- 特徵選擇(Feature Selection)
- 資料拆分(Data Splitting)
探索式資料分析
在進行 EDA 的初期,我們將首先檢視資料集中的所有特徵(資料欄位)及其對應的資料類型。
path = kagglehub.dataset_download("harlfoxem/housesalesprediction")
df_raw = pd.read_csv(f"{path}/kc_house_data.csv")
df_raw.info()
RangeIndex: 21613 entries, 0 to 21612 Data columns (total 21 columns):
| Column | Non-Null Count | Dtype |
|---|---|---|
| id | 21613 | int64 |
| date | 21613 | object |
| price | 21613 | float64 |
| bedrooms | 21613 | int64 |
| bathrooms | 21613 | float64 |
| sqft_living | 21613 | int64 |
| sqft_lot | 21613 | int64 |
| floors | 21613 | float64 |
| waterfront | 21613 | int64 |
| view | 21613 | int64 |
| condition | 21613 | int64 |
| grade | 21613 | int64 |
| sqft_above | 21613 | int64 |
| sqft_basement | 21613 | int64 |
| yr_built | 21613 | int64 |
| yr_renovated | 21613 | int64 |
| zipcode | 21613 | int64 |
| lat | 21613 | float64 |
| long | 21613 | float64 |
| sqft_living15 | 21613 | int64 |
| sqft_lot15 | 21613 | int64 |
這份資料集包含 21,613 筆房屋交易紀錄及 21 個特徵,而且所有的資料欄位均無缺失值。目標變數 price 為連續數值,所以這是一個房價預測的迴歸問題。下一步,我們要獲取各個數值資料欄位的統計摘要,快速了解各個資料欄位的集中趨勢、離散程度以及潛在的異常值。
另外,我們將移除 id、date 和 zipcode 欄位,因為:
id欄位為唯一的識別碼,不適合作為預測模型中的特徵。date欄位為日期時間格式(object類型),不適用於本次的簡單線性迴歸模型。zipcode欄位雖然以數值(int64)形式呈現,但其本質上代表的是地理區域或類別資訊,而非一個具有連續意義的數值變量。例如,郵遞區號的數值大小無法反映房價的高低。
df_cleaned = df_raw.drop(["id", "date", "zipcode"], axis=1)
df_cleaned.describe()
| index | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | lat | long | sqft_living15 | sqft_lot15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 | 21613.0 |
| mean | 540088.1417665294 | 3.37084162309721 | 2.1147573219821405 | 2079.8997362698374 | 15106.967565816869 | 1.4943089807060566 | 0.007541757275713691 | 0.23430342849211122 | 3.4094295100171195 | 7.656873178179799 | 1788.3906907879516 | 291.5090454818859 | 1971.0051357978994 | 84.40225790033776 | 47.56005251931708 | -122.21389640494147 | 1986.552491556008 | 12768.455651691113 |
| std | 367127.1964826997 | 0.9300618311474632 | 0.7701631572177287 | 918.4408970468115 | 41420.51151513528 | 0.5399888951423824 | 0.0865171977279032 | 0.7663175692736397 | 0.6507430463662665 | 1.1754587569743042 | 828.0909776519151 | 442.57504267744406 | 29.373410802390172 | 401.6792400190783 | 0.13856371024192457 | 0.14082834238139208 | 685.391304252777 | 27304.179631338575 |
| min | 75000.0 | 0.0 | 0.0 | 290.0 | 520.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 290.0 | 0.0 | 1900.0 | 0.0 | 47.1559 | -122.519 | 399.0 | 651.0 |
| 25% | 321950.0 | 3.0 | 1.75 | 1427.0 | 5040.0 | 1.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1190.0 | 0.0 | 1951.0 | 0.0 | 47.471 | -122.328 | 1490.0 | 5100.0 |
| 50% | 450000.0 | 3.0 | 2.25 | 1910.0 | 7618.0 | 1.5 | 0.0 | 0.0 | 3.0 | 7.0 | 1560.0 | 0.0 | 1975.0 | 0.0 | 47.5718 | -122.23 | 1840.0 | 7620.0 |
| 75% | 645000.0 | 4.0 | 2.5 | 2550.0 | 10688.0 | 2.0 | 0.0 | 0.0 | 4.0 | 8.0 | 2210.0 | 560.0 | 1997.0 | 0.0 | 47.678 | -122.125 | 2360.0 | 10083.0 |
| max | 7700000.0 | 33.0 | 8.0 | 13540.0 | 1651359.0 | 3.5 | 1.0 | 4.0 | 5.0 | 13.0 | 9410.0 | 4820.0 | 2015.0 | 2015.0 | 47.7776 | -121.315 | 6210.0 | 871200.0 |
根據統計摘要,bedrooms(房間數)的最大值為 33,此數值看起來相當異常。這可能是資料輸入錯誤,或是代表一棟極大的房屋。讓我們進一步檢查該筆資料以釐清其真實性。
df_cleaned[df_cleaned["bedrooms"] == 33]
| index | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15870 | 640000.0 | 33 | 1.75 | 1620 | 6000 | 1.0 | 0 | 0 | 5 | 7 | 1040 | 580 | 1947 | 0 | 98103 | 47.6878 | -122.331 | 1330 | 4700 |
我們發現一筆資料顯示,1,620 平方英尺(約 150.50 平方公尺,46.45 坪)的居住空間竟有 33 間房間。這顯然是資料輸入錯誤,因此我們將刪除此筆資料。
df_cleaned = df_cleaned.drop(index=15870)
df_cleaned.describe()
| index | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | lat | long | sqft_living15 | sqft_lot15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 | 21612.0 |
| mean | 540083.5187858597 | 3.369470664445678 | 2.1147741995187856 | 2079.9210161021656 | 15107.38895058301 | 1.49433185267444 | 0.007542106237275588 | 0.23431426985008327 | 3.4093559133814546 | 7.65690357208958 | 1788.4253192670737 | 291.4956968350916 | 1971.0062465297058 | 84.40616324264298 | 47.56004660836573 | -122.21389098648899 | 1986.5828706274292 | 12768.828983897834 |
| std | 367135.06126862235 | 0.9079817873290319 | 0.7701769788113926 | 918.4568179727936 | 41421.42349679372 | 0.5399909189837709 | 0.08651918418760121 | 0.7663336413695738 | 0.6506681457363164 | 1.1754774594782644 | 828.0944873955233 | 442.5809311799611 | 29.373636486079928 | 401.68812297868783 | 0.13856419107721143 | 0.14082934761084603 | 685.392609954429 | 27304.756179316624 |
| min | 75000.0 | 0.0 | 0.0 | 290.0 | 520.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 290.0 | 0.0 | 1900.0 | 0.0 | 47.1559 | -122.519 | 399.0 | 651.0 |
| 25% | 321837.5 | 3.0 | 1.75 | 1426.5 | 5040.0 | 1.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1190.0 | 0.0 | 1951.0 | 0.0 | 47.470974999999996 | -122.328 | 1490.0 | 5100.0 |
| 50% | 450000.0 | 3.0 | 2.25 | 1910.0 | 7619.0 | 1.5 | 0.0 | 0.0 | 3.0 | 7.0 | 1560.0 | 0.0 | 1975.0 | 0.0 | 47.5718 | -122.23 | 1840.0 | 7620.0 |
| 75% | 645000.0 | 4.0 | 2.5 | 2550.0 | 10688.25 | 2.0 | 0.0 | 0.0 | 4.0 | 8.0 | 2210.0 | 560.0 | 1997.0 | 0.0 | 47.678 | -122.125 | 2360.0 | 10083.25 |
| max | 7700000.0 | 11.0 | 8.0 | 13540.0 | 1651359.0 | 3.5 | 1.0 | 4.0 | 5.0 | 13.0 | 9410.0 | 4820.0 | 2015.0 | 2015.0 | 47.7776 | -121.315 | 6210.0 | 871200.0 |
上表顯示,錯誤輸入房間數的資料已成功移除。
特徵選擇
在眾多可用特徵中,我們首要任務是識別與房屋價格(price)關聯性最高的變數。為此,我們將對資料集中所有特徵與房屋價格進行相關性分析,並選取相關性最高的特徵作為簡單線性迴歸模型的單一預測變數。
df_cleaned.corrwith(df_cleaned["price"])
| Feature | Correlation |
|---|---|
| price | 1.000000 |
| bedrooms | 0.315445 |
| bathrooms | 0.525147 |
| sqft_living | 0.702047 |
| sqft_lot | 0.089664 |
| floors | 0.256811 |
| waterfront | 0.266371 |
| view | 0.397299 |
| condition | 0.036336 |
| grade | 0.667447 |
| sqft_above | 0.605591 |
| sqft_basement | 0.323812 |
| yr_built | 0.054023 |
| yr_renovated | 0.126437 |
| lat | 0.306998 |
| long | 0.021637 |
| sqft_living15 | 0.585404 |
| sqft_lot15 | 0.082451 |
相關性分析結果顯示,室內居住面積(sqft_living)與房屋價格的相關性最高,相關係數為 0.702047。因此,我們將選取 sqft_living 作為簡單線性迴歸模型的唯一預測特徵。
接著,我們利用 Matplotlib 繪製散佈圖,以視覺化方式探討特徵 sqft_living 與目標變數 price 之間的關係。
df_cleaned.plot(kind="scatter", x="sqft_living", y="price", xlabel="Living Space (sqft)", ylabel="Price ($)", color="g")
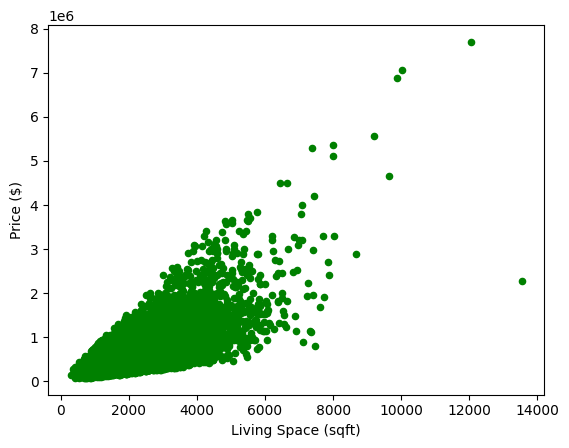
從圖表中可觀察到,大多數資料點集中於居住面積介於 500 至 6000 平方英尺、價格介於 50 萬至 200 萬美元的範圍內。居住面積與價格之間呈現顯著的正向關聯,即居住面積越大,價格越高。這表明回歸分析是合適的建模方法。儘管存在一些居住面積超過 10,000 平方英尺或價格超過 600 萬美元的離群值(Outliers),我們選擇不將其移除。這樣可以確保模型具備良好的泛化能力,使其仍能有效預測較大居住面積房屋的價格。
資料拆分
我們將利用 scikit-learn 函式庫中的 train_test_split 方法,將資料集劃分為訓練集(80%)和測試集(20%)。
x_train, x_test, y_train, y_test = train_test_split(df_cleaned["sqft_living"], df_cleaned["price"], test_size=0.2, random_state=23)
至此,資料處理階段已告一段落。
簡單線性迴歸模型設計
模型設計的核心在於選擇最能有效擬合原始資料的模型架構,以確保訓練後的模型能夠準確預測目標值,即房屋售價。
從上述資料分佈圖中,我們可以觀察到室內居住面積(sqft_living)與房屋售價(price)之間存在顯著的正向關係。儘管單純的線性模型可能無法完美擬合所有資料點,但為了便於理解機器學習模型的設計與訓練流程,我們仍選擇採用簡單線性迴歸模型作為本次實作的基礎。
以下列出本次模型設計所採用的關鍵組件與超參數:
| 模型組件 | |
|---|---|
| 模型架構(Model Architecture) | 簡單線性迴歸:ŷ = w * x + b |
| 損失函數(Loss Function) | 平均平方誤差(Mean Squared Error,MSE) |
| 超參數 | |
| 最佳化演算法(Optimizer) | 批次梯度下降(Batch Gradient Descent,BGD) |
| 學習率(Learning Rate) | 0.0000001 |
| 訓練週期(Training Epoch) | 10,000 |
表格中可能出現陌生的機器學習術語,不用擔心,我們將在後續的模型訓練環節中逐一進行解釋。
總而言之,模型設計的關鍵在於透徹理解問題的輸入與預期輸出,並深入分析資料集的內在分佈特性,進而選擇最能有效擬合資料並解決問題的模型架構。以預測房價為例,即是定義模型的輸入(室內居住面積)與輸出(房屋售價),分析兩者關係,於是選擇了簡化的簡單線性迴歸模型。
總結
- 本文介紹如何運用簡單線性迴歸模型預測房屋售價,目標是預估特定區域房屋的連續數值售價,並選擇「室內居住面積」(
sqft_living)作為唯一的預測特徵,因為它與房價(price)的相關性最高。 - 資料處理階段包含探索性資料分析(EDA),其中檢視了資料集特徵、處理了異常值(如33間臥室的房屋),並進行了特徵選擇和資料拆分(80%訓練集、20%測試集)。
- 模型設計採用簡單線性迴歸架構
ŷ = w * x + b,選擇平均平方誤差(MSE)作為損失函數,並使用批次梯度下降(Batch Gradient Descent)作為最佳化演算法,設定了學習率和訓練週期等超參數。
接下來,我們將深入探討模型訓練與評估的細節,請參考《房價預測模型:線性迴歸入門(下)》
