房價預測模型：線性迴歸入門（下）

本文為機器學習模型建構的入門教學，將介紹如何運用線性迴歸模型預測特定區域的房屋售價。在本文的下半部，我們將延續上半部對資料處理與模型設計的探討，深入闡述簡單線性迴歸模型的訓練與評估。我們將運用 NumPy 從頭實作訓練迴歸模型的核心演算法。此外，我們亦將介紹關鍵的評估指標，引導讀者客觀衡量模型效能。為確保內容的連貫性，如果你還沒有閱讀本文上半部，建議你先參考《房價預測模型：線性迴歸入門（上）》。

尋找參數的模型訓練

模型訓練的本質是尋找最佳模型參數的過程。其目標是找到一組參數，使得模型的預測值 ŷ 能夠最大程度地擬合真實資料集中的 y 值，即讓預測值盡可能接近真實數值。以上述預測房價為例，模型訓練的目標就是找出線性模型 ŷ = w * x + b 中的最佳模型參數 w（權重）和 b（偏差）。

損失函數

為了衡量模型預測值 ŷ 與真實值 y 之間的擬合（Model Fitting）程度，我們要引入一個目標函數（Objective Function），在建構機器學習模型時通常稱為損失函數（Loss Function）。其中一種常見且適用於迴歸模型的損失函數是平均平方誤差（Mean Squared Error，MSE），就是把所有的預估誤差值平方後加總平均：

$MSE = \frac{\sum_{i=0}^{n}(y_{true}^{(i)} - y_{pred}^{(i)})^2}{n}$

原則上，找出的模型參數讓 MSE 的值越小越好，這表示模型的預測值 ŷ 平均而言越接近真實值 y。而將預測誤差進行平方處理主要有兩個原因：

確保誤差為正： 確保所有誤差均為正值，避免正負誤差相互抵消，從而準確反映總體誤差。
可微分性： 如果使用絕對值而非平方，則無法對其進行微分，進而無法應用梯度下降等基於梯度的最佳化演算法來尋找最佳參數。

最佳化演算法：梯度下降

有了損失函數，我們就可以將訓練資料導入模型，並嘗試找到最適合的模型參數 w 和 b 值，以最小化 MSE。這個運算最佳化演算法的過程，就是機器學習模型訓練的核心。

將 ŷ = w * x + b 代入 MSE 公式並展開，我們可以得到：

$MSE = \frac{\sum_{i=1}^{n}(y_{true}^{(i)} - w * x_{true}^{(i)} - b)^2}{n}$

當我們將所有房屋交易訓練資料中的 x 和 y 值代入上述的 MSE 公式後，未知的參數就只剩下 w 和 b。我們的任務是找出能讓 MSE 值最小化的 w 和 b。如果我們暫時假設 b 為 0，則可以得到一個描述 w 與 MSE 之間關係的曲線圖形。讓我們首先專注於如何找到最佳的 w 值，然後再以此類推找到適合的 b 值。

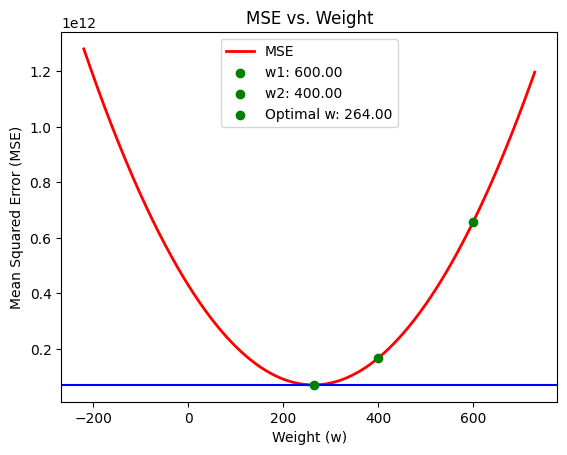
從上圖可以看出，MSE 的最小值位於曲線的凹點，此時 w 值約為 264。作為人類，我們一眼就能辨識出最佳化 MSE 函數的 w 值是 264，而非 400 或 600。

那麼，我們該如何讓電腦自動搜尋最佳的 w 數值呢？梯度下降（Gradient Descent）演算法正是為了解決這個問題而設計的。梯度下降演算法可以形象地比喻為盲人下山：「盲人無法看到整條下山的路徑，但他可以感知當前腳下的坡度與方向（梯度）。只要沿著坡度最陡峭的方向向下移動，他所經過的坡度就會越來越平緩，最終到達最平坦的地面。」這個目的地正是 MSE 值最小的地方，以上圖為例，即 w = 264 的位置。

在 MSE 函數中，特定位置的梯度（坡度與方向）就是 MSE 函數對 w 進行微分後的結果，也是瞬間的 MSE 改變率。其具體推導涉及基礎微積分，為保持文章的入門性質與流暢度，我們在此不深入探討。簡而言之，若要得知特定函數在特定位置的梯度，只需對該變數進行微分即可得到梯度函數。有了這個梯度函數，盲人就能知道在任意特定位置該往哪個方向走，最終成功下山。接下來，我們將實作一個簡單的批次梯度下降（Batch Gradient Descent，BGD）演算法，該演算法在每個訓練週期都會將所有訓練資料一次性引入梯度函數進行計算。

首先，讓我們計算參數 w 的梯度函數。我們可以使用 SymPy 庫，讓 MSE 函數對 w 進行微分，如下：

x, y, w = symbols("x, y, w")
mse_expr = (y - w * x) ** 2
dmse_dw_expr = diff(mse_expr, w) # -2 * x * (-w * x + y)

dmse_dw_fn = lambdify((x, y, w), dmse_dw_expr, 'numpy')
def compute_gradient_w(x, y, w):
    x = np.asarray(x)
    y = np.asarray(y)
    return np.mean(dmse_dw_fn(x, y, w))

$Gradien_{w} = \frac{\sum_{i=1}^{n}-2 * x_{true}^{(i)} * (- w * x_{true}^{(i)} + y_{true}^{(i)})}{n}$

其中，compute_gradient_w 函數可以用於計算特定 w 值下的梯度。接下來，我們就可以開始實作批次梯度下降演算法了，如下：

w = 600.0
L = .0000001
epochs = 100

for i in range(epochs):
    w -= L * compute_gradient_w(x_train, y_train, w, b)

程式碼中，w 被初始化為 600.0，以對應先前圖片中的範例。在實際應用中，更常見的做法是隨機設定一個起始點，然後利用梯度下降進行最佳化。

L 代表學習率（Learning Rate），它決定了在下山過程中每次移動的步長。在這裡，L 設定為 .0000001，這是因為在先前的實驗中發現梯度值非常大，若不設定較小的學習率，每次移動的步長會過大，導致無法有效收斂。在實務應用中，學習率的選擇通常需要透過實驗和調校來確定。許多專案會從 0.001 開始嘗試，直到找到最適合的學習率。若設定不當，則可能導致以下問題：

學習率過大： 可能導致模型在最佳解附近來回震盪，甚至發散，無法收斂。
學習率過小： 可能導致收斂速度過慢，大幅增加訓練時間。

每次參數更新的大小（下山的步長）由學習率 L 乘以梯度值決定。當梯度為正時，w 向負方向（左）移動；當梯度為負時，w 向正方向（右）移動，以實現 MSE 的最小化。epochs 則表示預計進行的訓練週期數（即下山的步數）。

值得注意的是，學習率 L 和訓練週期 epochs 這些超參數的選擇通常需要透過實驗和調校來確定。所謂的實驗，就是設定一組 L 和 epochs 數值，執行模型訓練，觀察 w 值是否收斂。所謂的收斂就是損失函數經由模型訓練降低到一定的程度，並且在訓練期間保持在特定的低點。而如果收斂，則表示我們可能已經找到適合的 w 值，使得 MSE 的值足夠小，並且模型能夠良好地擬合訓練資料。

完成整個訓練流程後，可以觀察到 w 值大約會收斂於 235 左右。接下來，我們將引入參數 b 進行訓練，同時優化 w 和 b 兩個參數，如下所示：

dmse_db_expr = diff(mse_expr, b)
dmse_db_fn = lambdify((x, y, w, b), dmse_db_expr, 'numpy')
def compute_gradient_b(x, y, w, b):
    x = np.asarray(x)
    y = np.asarray(y)
    return np.mean(dmse_db_fn(x, y, w, b))

w = 600.0
b = .0
L = .0000001
epochs = 10_000

for i in range(epochs):
    w -= L * compute_gradient_w(x_train, y_train, w, b)
    b -= L * compute_gradient_b(x_train, y_train, w, b)

透過上述模型訓練，我們得到優化後的參數為 w = 263.512825695545 和 b = -14.440659653819553。因此，最終的模型可以表示為 ŷ = 263.512825695545 * x - 14.440659653819553。現在，讓我們將模型與資料集一同繪製在平面上：

y = lambda x: w * x + b
x_values = np.linspace(0, 13540, 13541)
y_values = [y(x) for x in x_values]
plt.plot(x_values, y_values, color='r', linewidth=2)
plt.scatter(x_train, y_train, color="g")

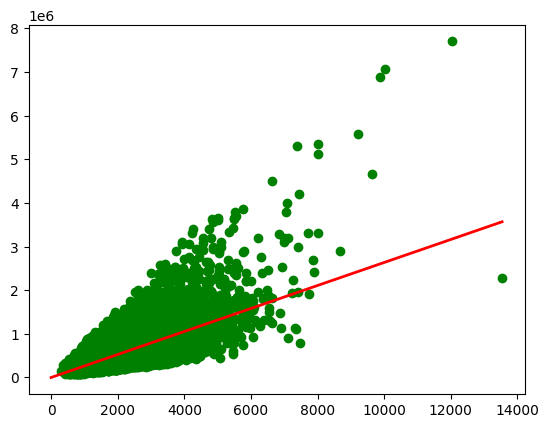
模型效能的評估

從上圖，我們能夠理解紅色的簡單線性迴歸模型無法有效地擬合訓練資料，因為有許多綠色的訓練資料點都在紅線之外，甚至有些點距離紅線非常遙遠。而模型評估的重點在於客觀地分析模型對訓練資料和測試資料的擬合程度。

正規化均方根誤差

均方誤差（Mean Squared Error, MSE）是衡量模型預測誤差的常用指標，它計算所有預測誤差值平方的平均值。然而，MSE 的單位是目標變數的平方，這使得其數值難以直觀解釋。為了將誤差恢復到與原始目標變數相同的單位，我們通常會對 MSE 取平方根，得到均方根誤差（Root Mean Squared Error, RMSE）。

$RMSE = \sqrt{MSE}$

雖然 RMSE 提供了模型預估的平均誤差金額，但單獨的 RMSE 值仍缺乏上下文，難以判斷其誤差是否過大。例如，一個為 $1,000 的 RMSE 值對於預測房價而言可能很小，但對於預測咖啡價格而言則非常的大。

為了解決 RMSE 缺乏上下文的問題，我們引入正規化均方根誤差（Normalized Root Mean Square Error, NRMSE）。NRMSE 的核心概念是將 RMSE 值對目標變數進行正規化，使其成為一個相對誤差指標，值越小越好，因為 NRMSE 總是大於等於 0。

在房價預測案例中，最直觀且常用的 NRMSE 計算方式是將 RMSE 除以實際觀測值（房屋價格）的平均值。其公式如下，其中是所有實際房屋價格的平均值：

$NRMSE = \frac{RMSE}{\bar{y}}$

現在，讓我們來計算我們訓練好的房價預測模型的 NRMSE：

nrmse_train = compute_mse(x_train, y_train, w, b) ** 0.5 / np.mean(y_train)
nrmse_test = compute_mse(x_test, y_test, w, b) ** 0.5 / np.mean(y_test)

計算結果顯示，訓練資料的 nrmse_train 約為 0.4895，而測試資料的 nrmse_test 約為 0.4671。這表示模型在訓練資料中的 NRMSE 為 48.95%，在測試資料中的 NRMSE 為 46.71%。

從經驗法則來看，我們可以根據 NRMSE 的數值區間來評估模型的效能：

極佳：小於 5%，表示模型預測非常精確，誤差極小。
良好：介於 5% 到 10%，表示模型表現良好且實用，誤差在可接受範圍內。
可接受：介於 10% 到 20%，表示模型具有一定的預測能力，但誤差相對較大。在某些情況下可能作為起點，但通常會尋求進一步優化。
需要改進：大於 20%，表示模型的預測能力較弱，結果可能不足以支持可靠的決策，需要對模型進行大幅度的改進。

根據上述經驗法則，並不是絕對值，主要是要考量業務目標和行業標準。在這裡我們先使用上述標準，模型的 NRMSE 值（約 48.95%）顯然屬於「需要改進」的範疇。這意味著模型的預測結果與實際值之間存在較大的偏差。例如，如果模型預估一棟房屋的價格為 50 萬美元，實際價格可能落在 25 萬美元（50 * (1 - 0.4895)）到 74 萬美元（50 * (1 + 0.4895)）之間，這樣的估算確實不具備足夠的參考價值。

擬合不足與過度擬合

在機器學習的模型評估中，當模型對訓練資料的預測能力不佳時，我們稱之為「擬合不足」（Underfitting）。反之，若模型能良好地預測訓練資料，卻無法有效預測未見過的測試資料，則稱之為「過度擬合」（Overfitting）。

如果模型出現擬合不足，通常是因為模型選擇不當或複雜度不足，導致其無法充分捕捉訓練資料的模式。此時，可考慮更換模型類型或增加模型複雜度（例如，增加模型參數量）以改善擬合效果。相對地，過度擬合則常因模型複雜度過高所致，儘管能完美擬合訓練資料，卻喪失了對新資料的泛化能力，導致測試表現不佳。面對過度擬合，可行的解決方案包括降低模型複雜度（例如，減少模型參數量）或擴充訓練資料集。

在機器學習模型的建構過程中，持續的實驗至關重要，旨在探索最佳的模型架構與超參數組合，以達到理想的性能。就本範例而言，儘管我們訓練出的模型存在擬合不足的現象，但本次展示的重點在於呈現模型訓練與評估的具體流程，因此將不再進一步進行模型改良的實驗。

總結

模型訓練與參數尋找：文章闡述了線性迴歸模型訓練的核心，即透過最小化損失函數（如平均平方誤差 MSE）來尋找最佳模型參數（權重 w 和偏差 b）。
梯度下降演算法：詳細介紹了梯度下降（Gradient Descent）作為最佳化演算法，它透過計算損失函數的梯度並乘以學習率（Learning Rate）來迭代更新參數，以逐步逼近損失函數的最小值。
模型效能評估：模型效能透過均方根誤差（RMSE）和正規化均方根誤差（NRMSE）進行評估。房價預測模型的高 NRMSE 值（約 48.95%）顯示其存在「擬合不足」（Underfitting）問題，表示模型過於簡單，未能有效捕捉資料模式。